See also: IBM Systems Journal paper http://www.research.ibm.com/journal/sj/393/part1/gerasimov.html
by V. Gerasimov and W. Bender
Sound is explored as an inter-device communication medium. Considerations include robustness in various environments, potential interference, frequency limitations of conventional and piezoelectric devices, computational complexity, and strategies for ultrasonic and human audible frequencies. Algorithms include modem protocols, data hiding techniques, impulse coding, and dual tone modulation.
Why does a phone ring not tell your computer who is calling? Why does your wrist-watch alarm not signal your oven to turn off? Many commonplace devices and appliances contain information that can be shared with others. While many of these devices have mechanisms, e.g., audio or video, to transfer information to people, they are deficient in their ability to communicate information that can be important to other devices. For example, almost all modern electronic devices have internal clocks, but are incapable of automatically transferring the time and date settings from one device to another. ``Things That Talk'' research focuses on the use of sound to enable device-to-device communication.
Sound in device-to-device communication
Sound signals and the environment
Sound is radiant energy that is transmitted in longitudinal waves that consist of alternating compressions and rarefactions in a medium. The maximum possible
frequency of sound in any medium is about 
. The speed of sound is dependent upon properties of the material through which it travels (see Table
1). Sound has propagation features quite different from that of light, which make an excellent alternative in situations where light does not work well. For example,
because sound travels slowly, the Doppler effect is strong enough to be used for motion detection of the relatively slow moving objects around us.
Many animals use high-frequency sound to detect the position and speed of objects in their environment (see Table 2). This method of orientation is called echolocation. It is especially useful for animals such as bats, which live in dark caves and need to hunt for insects at night, and whales, which spend their lives in turbid water. Humans have not overlooked this property of sound. In medicine, low-power ultrasonic waves (300 kHz) are used in place of X-rays to image internal body structures. Focused ultrasound can cause localized heating and destroy bacteria or tissue without harmful effect on surrounding tissue. Ultrasonic (100-16,000 MHz) microscopy1 provides better resolution than optical microscopy, and enables the investigation of a wide range of material properties in amazing detail. An important advantage of ultrasonic microscopes is their ability to distinguish between different parts of a live cell by viscosity. Also, because sound has minimal affect on the function of live cells, ultrasonic microscopy is used to study living cells. Finally, ultrasonic sonars are widely used for underwater exploration.
| Medium | Speed (meters/second) |
|---|---|
| Air at 0°C | 331 (increases with temperature and pressure) |
| Water | 1400-1600 (increases with temperature, salinity, and depth) |
| Lead | 1210 |
| Rolled aluminum | 5000 |
| Species | Frequency Range | Wavelength Range |
|---|---|---|
| Whales | 50-200 kHz (water) | 7-32 mm |
| Bats | 20-80 kHz (air) | 4-11 mm |
| Species | Frequency (Hz) | |
|---|---|---|
| low | high | |
| Humans | 20 | 20,000 |
| Cats | 100 | 32,000 |
| Dogs | 40 | 46,000 |
| Elephants | 16 | 12,000 |
| Bats | 1,000 | 150,000 |
| Grasshoppers | 100 | 50,000 |
| Rodents | 1,000 | 100,000 |
| Whales and Dolphins | 70 | 200,000 |
In contrast to these specialized imaging applications, sound in computers and communications applications has been limited to music, simple sound effects, and speech synthesis and recognition. (Notable exceptions include dual tone modulation (DTMF) used in telephony and phase-shift-keying (FSK) used in modems and facsimile machines. In fact, modems and faxes are pseudo-acoustic devices and cannot effectively communicate through air. They work well only with electric signals and require a wire to isolate the system from external disturbances.) Sound may be a good alternative for optical computer vision; for example, rather than trying to recognize people by imaging their faces or fingers in visible light, sonar technology can be used to measure unique body parameters, such as volumes, shapes, and locations of different organs.
Many electronic devices in and around the man-made environment are designed to speak and/or listen. Many devices have a speaker or beeper to relay status to a human. Some of these devices, such as telephones or faxes, have microphones. Piezoelectric beepers in wristwatches can also be used as microphones.[2]
This paper explores the use of sound as an inter-device communication medium. Considerations include robustness in various environments, potential interference, frequency limitations of conventional and piezoelectric devices, computational complexity, and strategies for ultrasonic and human audible frequencies.
Sound has many positive features that make it an attractive alternative to infrared light (IR) and radio frequencies (RF) for device-to-device communication. Humans (and most of the other living beings) use sound to communicate. Therefore, sound is a likely choice wherever people live or work. The human environment is usually designed to localize and preserve sound, and in such environments, sound is more predictable than IR and RF. Sound, unlike IR and RF, does not have unexpected foes such as sunlight, rain, metal objects, etc. Sound can be hidden from people if its frequency is higher than 20,000 Hz (see Table 3). IR usually requires direct visibility, and does not work in sunlight or bright interior light. Also, IR has some unexpected features. For example, it propagates through materials that are not transparent in visible light, and reflects from different materials than visible light. RF suffers from interference problems, and can be blocked by metallic objects. Sound does not have these problems. It travels around corners, and can still be localized within a room.
However, one feature of sound makes it difficult to analyze - sound travels slowly (about 300 meters/second in air). This creates several problems: (1) A signal reaches its target with a noticeable delay; and (2) Reflections of the signal from walls or other objects can be comparable in intensity to the original signal, and can reach the receiver with different delays, interfering with the main signal. (Due to the slow speed of sound, an echo may create long disturbances of the signal, making it necessary to use relatively long coding packets.) Other problems include the non-linear characteristics of most audio equipment that tend to shift signal phase and environments that have very different and practically unpredictable acoustic characteristics. Since the environment has little effect upon the relative amplitude of a sound within narrow bands of frequency, spectral analysis is a reliable method of acoustic signal analysis in unknown environments. These relative amplitude changes of the spectral components of a transmitted signal can be detected by a receiver.
Audible sound and lower-frequency ultrasound have similar features. Many small speakers and microphones used in electronic devices perform reasonably well at frequencies up to 30,000 Hz. The frequency limit of piezoelectric devices is much higher. This means that the same devices can use ultrasound whenever inter-device communication is not relevant for people and might be distracting or disturbing.
Sound signals have several convenient mathematical representations. Each representation splits the received sound signal to a function of the original signal plus noise:
Equation 1.
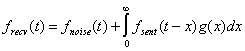
A received signal can be represented as a sum of the convolution of the transmitted signal with an impulse response of the environment and noise [3] (Equation
1). The lower bound in the convolution integral can be set to zero, since the system does not predict the future. Unfortunately, whenever air or any objects in a
given environment move, the parameters of the system change, and as a result, the impulse response may change in time. Therefore, g(x) depends on t. g(x)
cannot be calculated at the source and then used to analyze or predict the received signal. However, in any environment that can be used for acoustic
communication, g(x) has to decrease exponentially as 
. Also the integral of g(x) over the whole axis must be less or equal to 1.
The noise component in Equation 1 represents both the deviation of the system behavior from the regular convolution formula due to non-linearities and all other sources of sound in the environment. Noise is uncontrollable and unpredictable.
An impulse function gives the most complete description of an environment. Unfortunately, numerical methods that can find an impulse function and deconvolve a signal are not yet well developed, and modern computers are not yet fast enough to process signals at that level of abstraction in real time.
It is possible to use a simpler representation of the received signal. The original signal can reach the receiver either directly or after reflection from one or more surfaces. Therefore, the received signal can be represented as a sum of the directly received signals; all reflections (echoes) of the original signal that reach the receiver; and noise:
Equation 2. Where 
is an energy reduction coefficient and 
is the corresponding delay of a reflected or directly received signal.
Equation 2 has some useful features that help to explain why spectral analysis works in this kind of tasks. If the original signal is a sine wave, the sum of all reflections of the original signal is also a sine wave of the same frequency [4] (Equation 3). The amplitude of the reflected signal is proportional to the amplitude of the original signal, while its phase is hard to predict. In the worst case the resulting amplitude can be constant zero. This happens if the receiver (microphone) is exactly at a trough of the interference pattern produced by the wave in the environment. Though it is theoretically possible, the probability of this occurring in a real environment is extremely low.
Equation 3.
Any even signal can be broken down into a sum of sine waves. The spectrum of the signal gives the amplitudes of those waves. According to the previous results, all components of the spectrum of the received signal are proportional to the corresponding components of the spectrum of the source signal. Therefore, the spectrum of the original signal can be estimated using the spectrum of the received signal.
The Fourier transform allows the system to calculate the spectrum of a signal. However, if the sender uses only a few frequencies to encode data, there is not much sense in calculating the whole spectrum. It is sufficient to calculate only the Fourier coefficients that correspond to the coding frequencies.
Since sound reflects differently from different objects and propagates rather slowly, a sharp change in the original signal spectrum will cause several changes in the received signal spectrum. The receiver can correctly analyze the signal only after a certain amount of time known as the settle time. Therefore, a system can work only if either coding frames are longer than the average settle time, or it has an adequate echo tolerance reserve. Although the detectable echo tail in a medium-size room can be as much as several seconds long, the strongest echo components are the first reflections from large surfaces, e.g., walls, floor, ceiling, furniture, etc. The strongest echo components in a room usually have delays only up to several hundredths of a second.
Acoustic computer communication requires development of special protocols. The protocols used in modems, faxes, telephones, and remote controls are designed for mediums other than sound. However, all those protocols can be modified to work reliably with acoustic signals.
Modem protocols. An obvious first step in this research is to adopt existing fax/modem protocols for acoustic transmission. The fastest modem protocols exploit almost all of the properties of existing telephone lines. They rely on phase information; and they do not tolerate multiple echoes. Less sophisticated modem protocols (up to 2400 bps) are less dependent upon specific telephone-line characteristics and can be modified for use with through the air communication.
The audio signal stream in low speed modem protocols consists of a sequence of short coding frames. The transmitter generates several predefined frames that must be recognized by the receiver. All of the coding frames have the same length. Different coding frames must have different spectral characteristics to be distinguished by the receiver.3,5 Coding frames can contain either a single frequency, or a mixture of several frequencies. A simple technique used in modems is FSK, which uses single-frequency frames. The FSK frequencies are chosen so that there are a whole number of waves per frame and the frames can be easily distinguished by the receiver.
Usually, after traveling through the air, the signal is blurred because of echoes. A technique for circumventing this echo problem is to increase the frame length beyond the average echo settle time. Echo tolerance can also be increased by adjusting the coding frequencies used in adjacent frames.
Data-hiding protocols. Bender et al.6 suggest several possible techniques for adding recoverable inaudible data to a host acoustic signal. Spread-spectrum and phase encoding are useful for digital or high-quality analog transfers. One of their suggested techniques, echo coding, preserves hidden data after the sound has traveled by air.
Impulse protocols. To send data, IR remote controls use a sequence of light bursts with different delays between them. This method can be used with sound. An acoustic remote control can send short impulses with pauses between them. This protocol is easy to implement and requires minimal processing to recover the data. But it cannot deliver high continuous data transfer rates.
Touch-tones. Touch-tones used to dial telephone numbers and send information among telephone nodes work fine in air, but are slow and subject to noise. However, it is a ready-to-use method for computers to communicate with telephones and faxes. Recognition and generation algorithms are easy to implement. Each touch-tone code is a mixture of two tones chosen from a set of eight basic tones. Table 4 lists the standard telephone codes. The digits, ``*'', and ``#'' are used to dial numbers and ``A''-''D'' are used as special signals.
A personal computer (PC) sound board can be programmed to communicate with touch-tones. Patterns generated for each touch-tone code can be sent to the sound driver when the user presses the corresponding buttons. The recognition algorithm uses eight digital filters to detect basic tones. The touch-tones work well if they are at least 20 ms long. Thus, the maximum reliable data transmission speed that can be achieved using touch-tones is about 200 baud. The standard touch-tones are 70 ms or longer, which is above an average echo settle time. Therefore, computers, telephones, and faxes can communicate reliably using touch-tones. The set of tones used in this protocol can be expanded to achieve higher data transfer rates.
| 1209 Hz | 1336 Hz | 1477 Hz | 1633 Hz | |
| 697 Hz | 1 | 2 | 3 | A |
| 770 Hz | 4 | 5 | 6 | B |
| 852 Hz | 7 | 8 | 9 | C |
| 941 Hz | * | 0 | # | D |
The Things That Talk research is an exploration of different data encoding schemes for acoustic data transmission. In order to verify robustness of the protocols, several working prototype systems were built that use sound to communicate.
Echo coding. In the echo coding experiments, a one-bit modulation was used. An echo added to a signal corresponds to one and subtracted from the signal corresponds to zero:
Equation 4. Echo modulation. Where
is the echo delay; 
is the echo/signal ratio; 
is the encoded bit.
If the synthetic echo should change its sign abruptly, any change from zero to one or from one to zero will result in a click. A way to avoid these clicks is to increase and decrease the echo component linearly at either side of each frame.
There are several methods of detecting an echo with a given delay. The most robust methods require a Fourier transform of the signal and an analysis of its spectrum. Consequently, these methods need a great deal of processing power. Since one goal of this research is to use sound in ``ordinary'' devices, it is desirable to find methods of only modest computational complexity. A simplified echo coding method that requires only one multiplication per sample was developed:
Equation 5. Echo detection. Where 
is the sampling period; 
is the echo delay; 
is the number of samples used by the filter.
When a modulated signal is fed to the filter, the filter value can be presented as a sum of two components:
Equation 6. Filtering of a modulated signal.
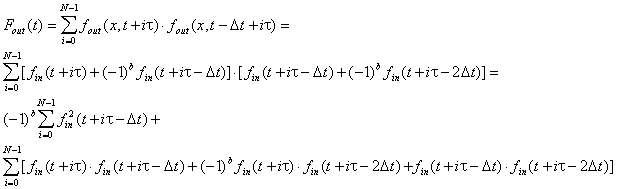
The first component is a sum-of-squares of the original function, and the second component is a sum-of-products of the original function at different points. The detection of echo is based on the fact that the absolute value of the first component is usually greater than the absolute value of the second component. The sign of the filter output is defined by the encoded bit.
The program does not analyze the original signal, and, therefore, may have poor results if the signal contains pauses or resonance frequencies. It is necessary to use an error correction code and to verify check-sums to support reliable data transfers.
Experiments with echo coding indicated that this method can give positive results at speeds of up to 100 baud, but it requires too much computational power to implement a robust real time communication protocol. Although the simplified echo detection algorithm is fast enough to work in real time on 8 MHz computers, its noise tolerance and signal independence leave something to be desired. The algorithm can reliably recover only about ten bits/second. However, since the coding frame size is longer than an expected echo tail in a room, this method does not degrade due to echoes in the environment.
The principle advantage of the echo coding technique is that it adds information to any acoustic signal in an audible spectrum (speech, music, noise), so that people do not clearly distinguish the communication between devices. One possible use of echo coding is to mix a message for people with a message for devices.
Echo coding has the three problems. First, silence has no echo, therefore the echo coding technique will not work well with signals that contain pauses. Silence can be avoided by adding noise to the signal, but this has the potential of spoiling the quality of the sound. An ultrasonic tone can be added to the signal, but receiving ultrasound requires special equipment. Second, speech and music may have fragments that resemble an echo. For example, if the original signal is a sine-wave and the chosen echo delay is equal to an integer number of the signal wavelength, an echo-like fragment results. Last, the echo coding does not completely hide the data signal since humans can detect even very weak echoes.
Phase-shift-keying and amplitude modulation. Two protocols based upon variants of FSK and amplitude modulation were developed. The first protocol uses frames of two frequencies to transmit four bits at simultaneously. 64 byte packets are sent as a synchronous sequence of four-bit frames, demarcated by a hail frame at the start of each sequence. The receiver, upon recognizing the hail signal, attempts to synchronize with the incoming data. Once synchronization is achieved, 64 bytes of information are transmitted. The system uses a partial Fourier transform to identify frequency patterns in the received signal. The second protocol uses an amplitude modulated 18.4 kHz sound signal. Again, a hail signal is used for synchronization. Data is sent as a set of one bit frames. Both protocols are implemented as part of Sonicom, a device-to-device communications prototype that uses a sound board to send and receive signals. Sonicom transfers data at speeds of up to 1.4 kbaud (see Tables 5 and 6).
| Transmitter output | 1 channel, 8-bit, 44,100 samples/second |
| Receiver input | 1 channel, 16-bit, 44,100 samples/second |
| Frame size | 120 samples: ~2.72 ms |
| Coding frequencies | 735 Hz, 1470 Hz, 2205 Hz, 2940 Hz, 3675 Hz, 4410 Hz |
| Hail frequency | 5512.5 Hz |
| Encoding | 4 bits/frame |
| Transmission speed | 1470 baud |
| Transmitter output | 1 channel, 8-bit, 44,100 samples/second |
| Receiver input | 1 channel, 16-bit, 44,100 samples/second |
| Frame size | 30 samples: ~0.68 ms |
| Coding frequency | 18,375 Hz |
| Hail frequency | 5512.5 Hz |
| Encoding | 1 bits/frame |
| Transmission speed | 1470 baud |
The Sonicom transmitter program generates and holds samples for each coding frame. The two-frequency protocol uses two tones to encode four bits. Each frame is comprised of either two different tones mixed together or silence (see Figures 1 and 2).
In order to define sixteen different frames (four bits), the system uses six different frequencies. There are 
frames composited from pairs of frequencies.
The sixteenth frame is silence.
Figure1. A packet is comprised of the hail signal and 16 different coding frames.
Figure 2. The same packet, after traveling approximately 1 meter through air, includes noise and echo added by the environment
Figure 3. Sonicom data transfer and receive methods.
A hail frame designates the beginning of each data packet (128 frames). Hail frames use a different frequency than data frames. This ensures that the receiver is able to readily identify the synchronization impulses.
All of the frames are multiplied by the Blackman function [3] (which is often used as a framing function in discrete Fourier analysis):
Equation 7. The Blackman function: 
is the frame width.
Performance is improved when the Blackman function is used by the transmitter to form frames. Use of the Blackman function also reduces the number of calculations required in the receiver.
In general, it is always better to encode data using as few discrete frequencies as possible. Fewer numbers of frequencies require fewer numbers of filters, thereby reducing the amount of computation necessary to decode a signal. Also, using fewer frequencies improves the overall frequency separation and noise tolerance of the system.
It is possible to define four bits using only five frequencies: 
frequency pairs, five single frequencies, and silence. In practice, it is problematic to clearly
recognize single frequency packets because of echo from packets transmitted earlier. The six-frequency scheme proved to be more tolerant of echo and noise.
The amplitude protocol uses a high-frequency (ultrasonic) tone to encode data (see Table 6). The data frames are 30 samples wide at 44.1 kHz. With this protocol, each frame represents only one bit. Typical computer microphones and speakers can handle frequencies up to about 30 kHz, but amplifiers and digital-to-analog converters (D/As) and analog-to-digital converters (A/Ds) have a limit of approximately 22 kHz. Conventional sound boards have maximum sampling rates of 44.1 kHz. However, they do not work well at this upper limit. A 18,375 Hz tone was chosen to correspond to one. Silence was used to correspond to zero. The same hailing frequency was used as in the two-frequency protocol. At 5.5 kHz, it was audible. This is adequate for a demonstration system, but must be increased if the protocol is to be truly ultrasonic.
The Sonicom receiver program conveys data from the sound board driver to a set of digital filters.7 The system uses the filter outputs to detect and decode incoming data. The receiver program maintains an idle state when no incoming packets are detected. When in this idle state, the system uses only the one filter that is needed to detect the hailing frequency. When a hail frame is received, the filter output first increases and then decreases. This results in a peak that is one frame wide. By estimating the mid-point of the peak, the receiver is able to synchronize with the incoming data. It is only necessary to activate multiple filters in order to decode the incoming data packets. Thus, computational load is reduced between data transmissions.
The digital filters are written in assembler using the Intel 80386 command set. Fixed-point arithmetic is used, enabling the program to run in real-time on Intel 80486DX 33 MHz computers. The value of each filter is calculated by the formula [4]:
Equation 8. Filter function: 
is the length of filter in samples; 
is the filtering frequency; 
is the sampling frequency; 
is sample values.
The value of each filter is a squared amplitude of the fourier coefficient corresponding to the filtered frequency.
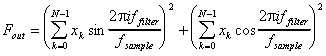
Filters are the most computationally expensive part of the system. The filter blocks are optimized so that they perform only three multiplication operations per filter per sample. The program calculates the values of sine and cosine during initialization and stores them in memory arrays for subsequent low cost filter state updates.
The Sonicom (see Figure 3) has good echo tolerance. This makes it possible to use a short frame size. The protocol works well with distances between transmitter and receiver of up to two meters (without obstacles). The reception improves if the receiver uses two microphones and sums the inputs.
A ``Battleship'' demonstration was prepared for the MIT Media Laboratory's Tenth Anniversary. Two PCs played Battleship with each other. The computers used sound to negotiate moves during the game. Two ``Talking Balloons''2 were used as speakers. The Battleship program implemented the traditional game rules. It displayed the game in progress as well as the comments sent and the messages received. The program used modules from Sonicom to send/receive and modulate/demodulate acoustic signals. Due to the poor acoustic properties of the balloons, two low-frequency tones were used for one-bit data encoding. Also, the frame width was increased. The balloons could have been used as microphones but were not because the quality was unsatisfactory. There was also a feedback problem when a single balloon was connected to a sound board as both a speaker and a microphone. Therefore, conventional microphones were used to receive sound.
Impulse coding. Another protocol, impulse coding, is similar to Morse code, but instead of using impulses of different length, it sends impulses of constant length with variable length pauses between them. The protocol encodes one bit at a time. The value of an encoded bit corresponds to the distance between two consecutive sound impulses. A short pause equals zero, and a long pause equals one (see Table 7). A similar protocol is implemented in IR remote controls. The protocol is easy to implement, requiring little computational overhead by either the sender or the receiver.
| Transmitter output | 1 channel, 1-bit, timer-modulated |
| Receiver input | 1 channel, 16-bit, 44,100 samples/second |
| Coding impulse width | ~5.7 ms (50 semiwaves) |
| Coding impulse frequency | 4,405 Hz |
| Bit 0 pause | ~5.7 ms (50 semiwaves) |
| Bit 1 pause | ~17 ms (150 semiwaves) |
| Average transmission speed | 59 baud (7-8 bytes/second) |
The receiver uses one digital filter to detect impulses. It dynamically adjusts its response level depending on the maximum filter output level from the last received impulse. The program measures the distance between the rising edges of two consecutive impulses. If the distance approximates the coding length of either a zero or a one, then the receiver adds the decoded bit to a buffer. Otherwise, it resets the buffer.
The impulse protocol is implemented on the handy-board (see Figure 4), [8] a computer developed by the Media Laboratory's Epistemology and Learning Group. It is capable of sending the contents of the notebook to other computers using sound. The board consists of a Motorola MC68HC11 CPU (8 MHz), 32K of static RAM, a 16x2 alpha-numeric LCD display, a speaker, an infrared receiver, an RS-232 serial port, several analog and digital input/output ports, several LEDs, two buttons, and a knob. The implementation has two parts: (1) A program for sending data using sound; and (2) a receiver in the form of PC programs that decode the sound signals sent by a handy-board.
The handy-board has been programmed as a clock and a notebook. The handy-board program sends out a notebook record using the built-in speaker. A receive program is run on a host computer to update the contents of the notebook.
The data transfer-rate of impulse coding is slower than protocols that use multifrequency encoding.
Figure 4. The handy-board
The impulse protocol suffers somewhat from echo, but otherwise proves to be reliable. However, if audible impulses are used, it creates a disturbing noise.
Both audible sound and ultrasound have a psycho-physiological effect on people. Audible sound probably can be used safely either in rather short data exchanges, when people may want to control the transmission (e.g., phone rings, acoustic remote controls, data exchange between wrist-watches and computers), or for long data exchanges, when people are not present. Ultrasound in the 20,000-500,000 Hz (and probably higher) range is harmless, if it is not very loud. If ultrasound is extremely intense, it may cause heating and scattering of hard objects. Noise at frequencies lower than 100,000 Hz may be unpleasant for pets. There are many natural sources of ultrasound, such as bats and some insects, that may produce very loud ultrasonic noise. These sounds do not seem to affect people or animals. Almost all television sets and computer monitors constantly squeak with line-scanning frequency, which has not been recognized as a source of medical problems.
Five subjects from the MIT Media Laboratory participated in a study conducted to determine which encoding techniques produced the least disturbing noise. Subjects listened to examples of DTMF, ultrasonic coding, FSK, impulse coding, and echo coding. As expected, since ultrasonic and echo coding techniques operate near the threshold of the human auditory system, all of the subjects found these the least disruptive.
Four subjects preferred touch-tones to other audible techniques. They explained that either they were accustomed to touch-tones or that the data transmission sounded melodic to them. One subject pointed out that since FSK has a much faster data transfer-rate than touch-tones, it might be preferable to listen to an FSK squeal for a short period of time rather than to touch-tones or impulse coding sounds for a longer period.
One could conclude that ultrasound should be used for device-to-device communication and that audible signals be sent only when devices communicate to people. The FSK modulation can be used ultrasonically, achieving even higher data transfer-rates than reported here. However, this will require special hardware, that can operate at higher sampling-rates than conventional sound boards or that can process sound signal in analog. Touch-tones are relatively attractive, not only because they are commonplace, but also because the combination of two frequencies produces a beat (characteristic pulsation) that makes sound alternately soft and loud. This is similar to the sounds produced by musical instruments. In moderation, the tones seem pleasant. Touch-tones are typically much longer than frames in FSK modulation. It explains why those data coding techniques sound so different to human observers. Perhaps, the attractiveness of double-frequency tones can be used to make an encoding that sounds like pleasant music. The only advantage of the impulse (remote control) modulation, which is used in the handy-board project, is its simplicity. It requires minimal acoustic hardware quality and processing power, and can be used in small devices with limited resources.
A wristwatch can use the sound from its beeper to transmit data to a computer. This may be of use as a communication back-channel for wristwatches that keep address and phone data. An airport public address announcement can transmit data for wristwatches, PDAs, or laptop computers. A computer may have an easier time than people in decoding the contents of those announcements.
Several computers close to the same wall, floor, ceiling, or table can use an acoustic transceiver to transfer data through a solid object. It would work as a ``wireless'' network. The sound would travel much faster and at higher frequencies than it does through air.
Three acoustic responders placed on a ceiling can serve as reference points to track the position of other objects in a room. A device that wants to know its position can send a ``ping'' to the responders, receive responses, measure time delays, and calculate the distances to each of the responders. This method can provide relative coordinates of the device with very high precision. The theoretical precision limit for digital processing with a typical sound board (44.1 K samples/second) is about 15 mm, but analog ultrasonic devices can achieve much better results. The advantage of this method over electromagnetic sensors is that all of the coordinate calculations are linear.
Echo encoding (10 baud)
DTMF (Dual Tone)
Sonicom two-frequency
Sonicom ultrasonic
Impulse coding
This work was supported in part by the Things That Think Consortium at the MIT Media Laboratory.
Vadim Gerasimov MIT Media Laboratory, 20 Ames Street, Cambridge, Massachusetts, 02139 (electronic mail: vadim@media.mit.edu). Mr. Gerasimov graduated with a Master of Science in Media Arts and Sciences from MIT in 1996.
Walter Bender MIT Media Laboratory, 20 Ames Street, Cambridge, Massachusetts, 02139 (electronic mail: walter@media.mit.edu). Mr. Bender is Associate Director of the MIT Media Laboratory and Director of the Laboratory's News in the Future Research Consortium.